Přístupy k určování párů

Jeden z předcházejících příspěvků „Principy práce s RelativeValues Lab„se věnoval stručnému popisu dílčích problémů, které by měl software pro tvorbu obchodní strategie založené na obchodním přístupu Relative Value, umožnit řešit. Klíčovým krokem takové strategie je identifikace dvojic dostatečně podobných aktiv. To je velmi nekonkrétní pojem a proto i tento krok lze realizovat různými postupy. Aby mohly být vyhledané dvojice co nejstabilnější, má smysl nejprve provést odfiltrování aktiv, která jsou pro párové obchodování nevhodná, protože mají jen velmi málo společného (technicky, ekonomicky, politicky atd.) i přes to, že jejich chování může být dočasně (náhodně) podobné. Prvotní výběr lze provést prostřednictvím různých snadno dostupných ukazatelů (deskriptivních a fundamentálních, ale i technické ukazatele lze pro tyto účely použít). Mezi předvybranými kandidáty se pak hledají dvojice těch, kteří se historicky dlouhodobě pohybovali co nejvíce společně.

I pro vlastní testování spolupohybů ve dvojicích časových řad lze použít několik postupů založených na různých matematických a statistických metodách:

• korelace změn hodnot – jedna z historicky prvních metod pro detekci potenciálních párů, která již byla stručně představena v jednom z předcházejících příspěvků „The Relative Value Approach“ a detailnější souhrn analýzy jejích výstupů byl uveden jiném příspěvku „Walk forward test of correlated pairs„
• minimalizace vzdáleností – spolupohyb je hledán jako nejnižší suma čtverců rozdílů normalizovaných řad
• kointegrační analýza – jedna řadu v páru je lineární kombinací druhé řady
• analýza náhodného rozpětí – předpokládá, že rozdíl cen osciluje kolem dlouhodobého průměru

Výstup analýzy korelací mezi změnami hodnot časové řady vypovídá o síle shody společných pohybů, takže řady s vysokou korelací změn hodnot se tak mohou vzájemně vzdalovat (např. obě rostou, přičemž jedna roste rychleji) a už se nemusí k sobě přiblížit.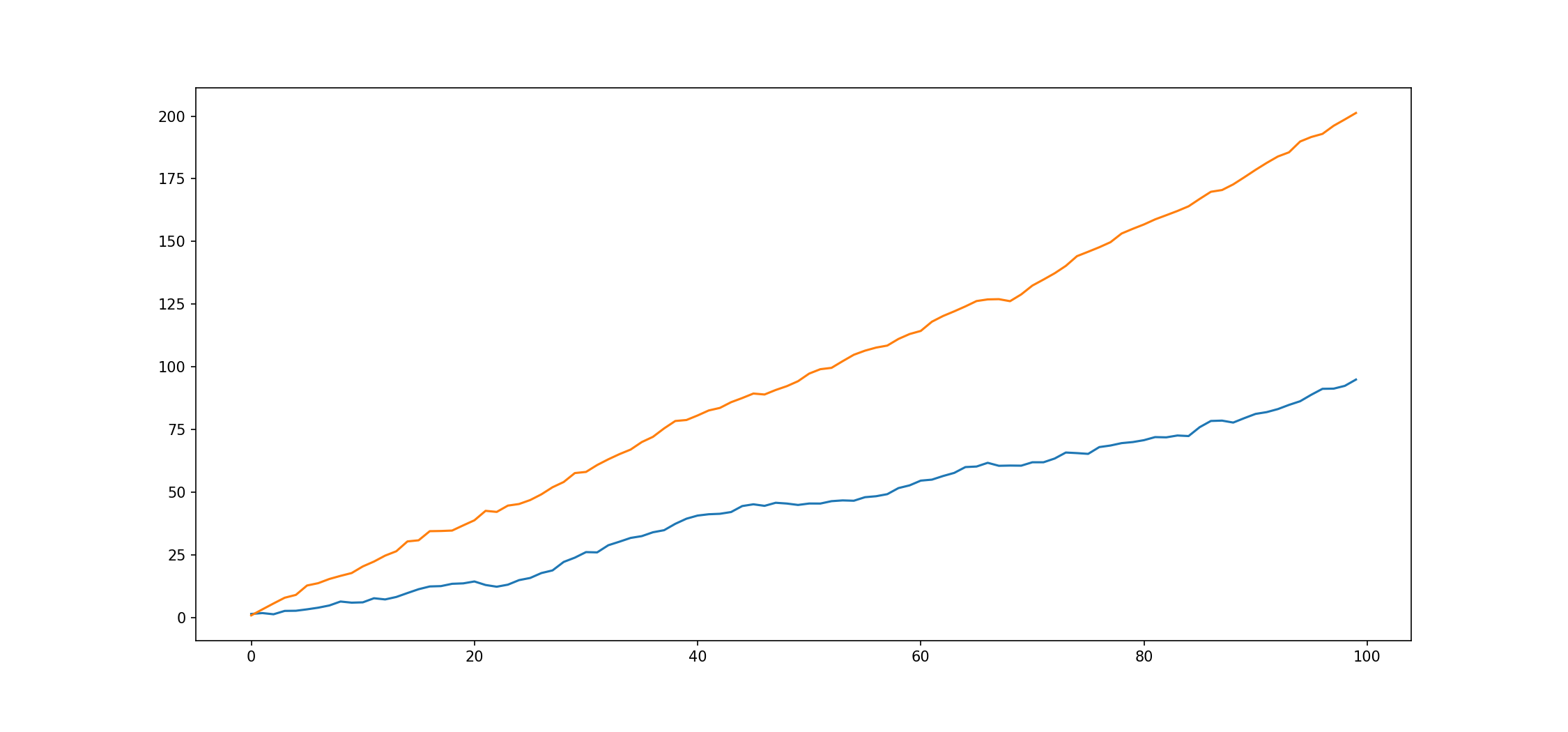Pro párové obchodování je však žádoucí situace, kdy časové řady se po dočasném oddálení vzájemně k sobě opět přiblíží, což přítomnost vysoké korelace změn hodnot nezaručuje. Tento jev vzájemného přitahování časových řad je schopna lépe identifikovat kointegrační analýza.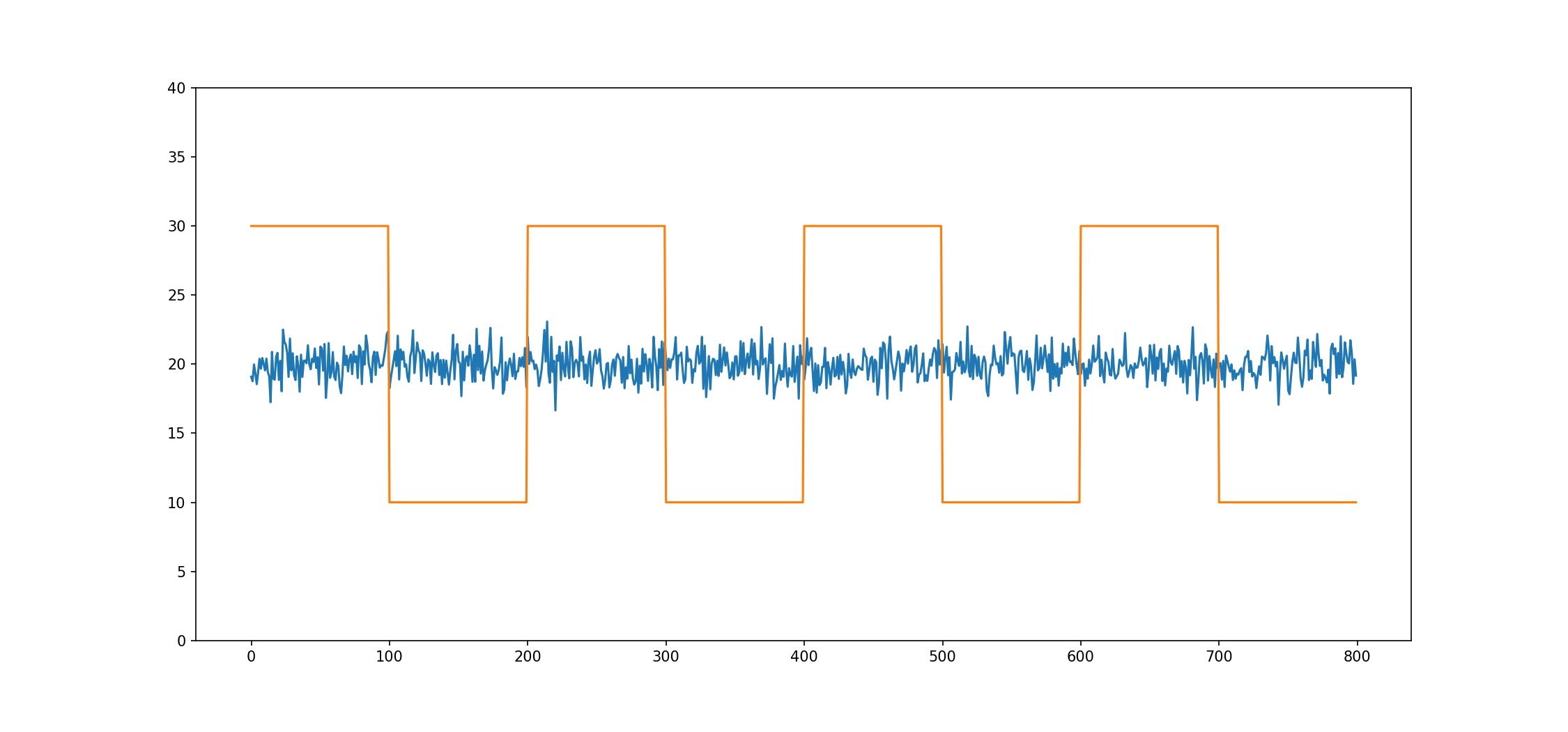Analýzu korelací změn hodnot tak lze použít jako jeden z prvotních filtrů pro výběr kandidátů, mezi nimiž jsou pak hledány dvojice vhodné pro párové obchodování.

Kointegrační analýza je nejběžnějším současným přístupem používaným k identifikaci párů. Opírá se o statistický koncept stacionárních náhodných procesů, což jsou procesy, které jsou bez trendu, mají s měnícím se časem stejný rozptyl a stejný průběh autokorelační funkce. Většina finančních časových řad však tyto vlastnosti nesplňuje, jde tedy o procesy nestacionární, přesto lze při hledání společného chování časových řad využít testování stacionarity.

Obecně platí, že lineární kombinace dvou nestacionárních časových řad vyústí opět v nestacionární časovou řadu. Pokud jsou ale časové řady generovány stejnými nebo velmi podobnými procesy, je možné, že některá lineární kombinace těchto řad vyústí ve stacionární řadu. Základní myšlenkou kointegrační analýzy je tedy nalezení takové dvojice nestacionárních časových řad, jejichž lineární kombinace vytvoří časovou řadu stacionární. Aby bylo možné považovat řady za kointegrované, rezidua z nalezené lineární kombinace řad musejí být stacionární.

Pro časové řady vstupující do analýzy se často, kvůli předpokladům pro použití určitých metod, používají různé transformace jako např. normalizace, logaritmy původních hodnot či klouzavé průměry. Nejznámější metodou pro hledání lineární kombinace je tzv. metoda nejmenších čtverců, lze však využít i tzv. metodu úplných nejmenších čtverců (ortogonální regresi). Testováním stacionarity řady (reziduí) se zabývá mnoho testů jednotkového kořene, nejznámějším zástupcem je ADF test, PP test či KPSS test. Pro kvalitnější rozhodnutí je vhodné provést KPSS test a některý z dalších testů tohoto typu (ADF). KPSS test se od ostatních liší konstrukcí nulové hypotézy (hledá důkazy pro nestacionaritu, zatímco ADF a další pro stacionaritu), pokud se testy shodnou, je velmi vysoká pravděpodobnost, že závěr skutečně platí.

Vedle testování stacionarity reziduí z nalezené lineární kombinace je vhodné provést i prostou analýzu frekvence návratů řady ke své střední hodnotě, resp. doby mezi dvěma protnutími. Výhodou této analýzy je skutečnost, že cílí přímo na konkrétní vlastnost řady, která je z praktického pohledu pro účely párového obchodování nejdůležitější. Nalezená dvojice vykazující stacionaritu reziduí může mít tak nízkou četnost návratů ke střední hodnotě, že pro párové obchodování bude nezajímavá, jelikož u takového páru by bylo nutné držet pozice otevřené příliš dlouhou dobu, což z pohledu řízení rizika může znamenat problém. Stacionarita sama o sobě zde tedy tak silný význam nemá, významnější je spíše jeden z jejích projevů: vysoká četnost návratů časové řady ke své střední hodnotě.

Po nalezení dvojic s vlastnostmi blížícími se ideálním požadavkům (s rezidui z lineární kombinace, která jsou stacionární a mají dostatečně vysokou frekvenci návratů ke střední hodnotě) lze však s jistotou předpokládat, že tyto vztahy nebudou trvat věčně. Za vhodné období pro opakování procesu hledání párů se běžně doporučuje uplynutí 6 měsíců.

Naďa Chalupová